Jak uzupełnić proporcję?

Pod względem matematyki proporcja jestrówność dwóch relacji. Współzależność jest charakterystyczna dla wszystkich części proporcji, a także ich niezmienionego wyniku. Aby zrozumieć, jak zrobić proporcję, można zapoznać się z właściwościami i formułą proporcji. Aby zrozumieć zasadę rozwiązywania proporcji wystarczy jeden przykład. Tylko bezpośrednio rozwiązując te proporcje, możesz łatwo i szybko nauczyć się tych umiejętności. I ten artykuł pomoże czytelnikowi w tym.

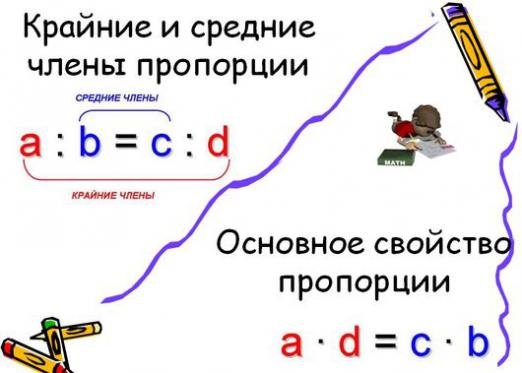
Właściwości proporcjonalne i formuła

1. Odwrócenie proporcji. W przypadku, gdy dane równanie wygląda jak 1a: 2b = 3c: 4d, napisz 2b: 1a = 4d: 3c. (I 1a, 2b, 3c i 4d są liczbami głównymi innymi niż 0).
2. Mnożenie danych warunków proporcjiw przekroju poprzecznym. W wyrażeniu alfabetycznym ma on postać: 1a: 2b = 3c: 4d, a wpis 1a4d = 2b3c będzie równoznaczny z tym. Tak więc iloczyn skrajnych części dowolnej proporcji (liczba na końcach równości) jest zawsze równa iloczynowi środkowych części (liczby znajdujące się w środku równości).
3. Podczas komponowania proporcji przydatna może być jej własność, taka jak przegrupowanie skrajnych i środkowych elementów. Wzór równości 1a: 2b = 3c: 4d może być reprezentowany przez takie warianty:
   • 1a: 3c = 2b: 4d (gdy średnie warunki proporcji są uporządkowane).
   • 4d: 2b = 3c: 1a (przy zmianie skrajnych warunków proporcji).
4. Doskonale pomaga w rozwiązywaniu proporcji swojej własności zwiększania i zmniejszania. Dla 1a: 2b = 3c: 4d, napisz:
   • (1a + 2b): 2b = (3c + 4d): 4d (równość przez zwiększenie proporcji).
   • (1a - 2b): 2b = (3c - 4d): 4d (równość przez zmniejszenie proporcji).
5. Możesz utworzyć proporcję, dodając i odejmując. Kiedy proporcja jest zapisana jako 1a: 2b = 3c: 4d, to:
   • (1a + 3c): (2b + 4d) = 1a: 2b = 3c: 4d (proporcja składa się z dodania).
   • (1a - 3c): (2b - 4d) = 1a: 2b = 3c: 4d (proporcja składa się z odejmowania).
6. Ponadto, przy rozwiązywaniu proporcji zawierających ułameklub duże liczby, możesz podzielić lub pomnożyć obu członków przez ten sam numer. Na przykład składowe proporcji 70: 40 = 320: 60 można zapisać w następujący sposób: 10 * (7: 4 = 32: 6).
7. Roztwór proporcji z procentami wyglądatak. Na przykład napisz, 30 = 100%, 12 = x. Teraz powinniśmy pomnożyć średnie terminy (12 * 100) i podzielić przez znaną ekstremum (30). Tak więc odpowiedź brzmi: x = 40%. W podobny sposób można wykonać mnożenie znane skrajne warunki, w razie potrzeby, aby podzielić je na określoną średnią liczbę uzyskując pożądany rezultat.

Jeśli interesuje Cię konkretna formuła proporcji,Następnie w najprostszym przykładzie wykonania, część i rozprowadzane oznacza związek (wzór): A / B = C / D, w tym a, b, c i d są cztery niezerowe liczby.