Jak znaleźć boki trapezu?

Szkolny kurs geometrii wymaga znajomościz wszelkiego rodzaju czworobokami, w tym z trapezami. Najbardziej podstawowymi zadaniami, które dotyczą trapezów, są poszukiwanie stron i połów. W tym artykule rozważymy kilka przykładów rozwiązywania problemów związanych ze znalezieniem boków trapezu.

Trapezes to:

arbitralne;
równoramienny;
prostokątny.

Rozwiązywanie problemów na dowolnym trapezie

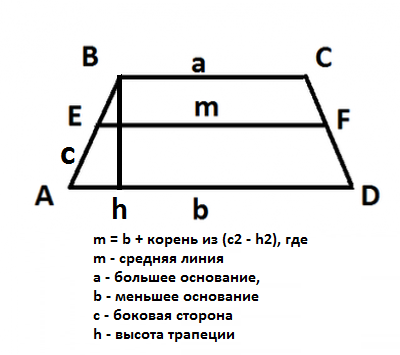
Trapezoid to czworobok z dwomaboki są równoległe, a te dwa nie. Określenie strony w dowolnym trapezoidzie zależy od danych początkowych. Rozważmy przypadek, w którym znane są kąty podstawy i wysokość.

Zadanie 1

Pokazano trapez ABCD, w którym wysokości VC i CM są równe 6 cm, a kąty u podstawy wynoszą 60 i 45 stopni. Wymagane jest znalezienie boków.

Mamy więc dwa trójkąty prostokątne AVKi SDM, którzy znają jedną nogę i przeciwległy kąt. Cynos (stosunek przeciwnej nogi do przeciwprostokątnej) dla 60 i 45 stopni jest znany: sin 60 = √3 / 2, a sin 45 = √2 / 2.

Otrzymujemy:

sin 60 = BK / AB, stąd AB = VK / sin 60
AB = 6 / √3 / 2 = 4√3 (cm)
sin 45 = CM / SD, stąd SD = CM / sin 45
LED = 6 / √2 / 2 = 6√2 (cm)

Odpowiedź: AB = 4√3 cm i SD = 6√2 cm

Rozwiązanie problemów na prostokątnym trapezie

Prostokąt to trapez, którego kąty na jednym z boków są równe 90⁰. Zastanów się, jak znaleźć bok trapezu, jeśli znane są pozostałe trzy boki.

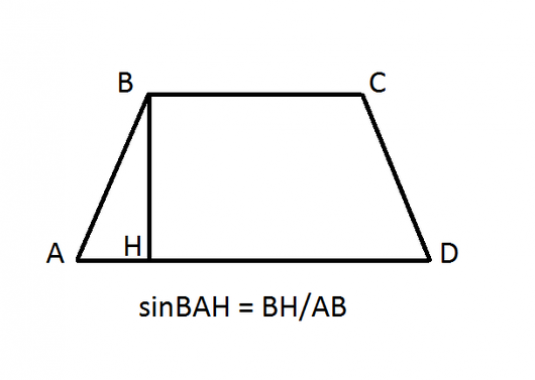
Problem 2. Podano trzy boki, z których jeden jest prostopadły z boku.

Załóżmy, że otrzymaliśmy prostokątny trapezowy ABCD, w którym AB jest prostopadła do BC. Wiadomo, że AB = 12 cm, BC = 1 cm, AD = 6 cm Należy znaleźć duży bok boczny.

Rozwiązanie:

Z punktu C pominąć wysokości ładowni Wielkiej Brytanii i uzyskać prawo trójkąta i prostokąta ABCK KFOR. Ponieważ przeciwległe boki prostokąta to CK = AB = 12 cm, a AK = BC = 1 cm.

Znaleźliśmy segment KD:

CD = AD - AK = 6 - 1 = 5 (cm)

Zgodnie z twierdzeniem Pitagorasa:

LED²= SK²+ CD²= 12²5²= 144 + 25 = 169
LED = √169 = 13 (cm)

Odpowiedź: LED = 13 cm

Problem 3. Biorąc pod uwagę podstawy i kąt u podstawy

Biorąc pod uwagę trapezoidalne ABCD, w którym podstawy słońca i ciśnienie krwi wynoszą odpowiednio 6 i 10 cm, kąt VAD jest prosty, a SDA wynosi 45 stopni. Znajdź mniejszą stronę.

Narysujemy wysokość SC i otrzymamy prostokątny trójkąt SKD i prostokąt ABCS. Ponieważ przeciwległe boki prostokąta to AK = BC = 6 cm.
CD = AD - AK = 10 - 6 = 4 cm
cos 45 = √2 / 2 = CD / LED, stąd CD = CD / cos 45
Otrzymujemy SD = 4 / √2 / 2 = 4√2 (cm)

Odpowiedź: SD = 4√2 cm

Rozwiązywanie problemów trapezu równoramiennego

Trapezoid nazywa się równoramiennikiem, którego boki są równe. Aby zrozumieć, jak je znaleźć, rozważ następujące przykłady

Problem 4. Podano zarówno podstawy, jak i wysokości

Biorąc pod uwagę trapezowe ABCD, w którym AB = SD, i VC i CM - wysokości. BC = 9 cm, AD = 19 cm, a BK = CM = 12 cm Znajdź stronę.

Daj nam udowodnić, że trójkąty ABK i DSM są równe. Według warunku AB = CD, BK = CM. Ponieważ trapez jest równoramienny, kąty BAC i SDM są równe. Ponieważ VC i CM są wysokościami, te trójkąty są prostokątne. Stąd AVC k = 180 - (90 + HAC), a kąt DPA = 180 - (90 + SDM), jak również WAC i SDM są sobie równe, wówczas również AVC i MSD. Zatem trójkąty AVK i DSM i DSM są równe po obu stronach i kąt między nimi.

Znajdujemy segmenty AK i MD.