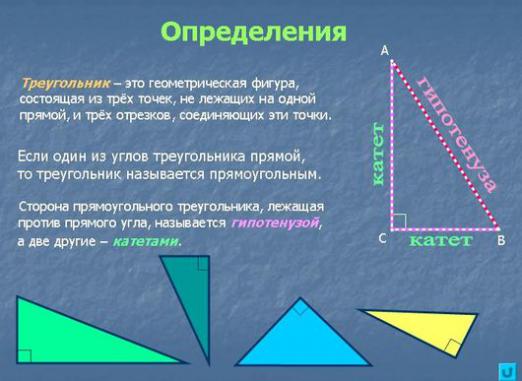
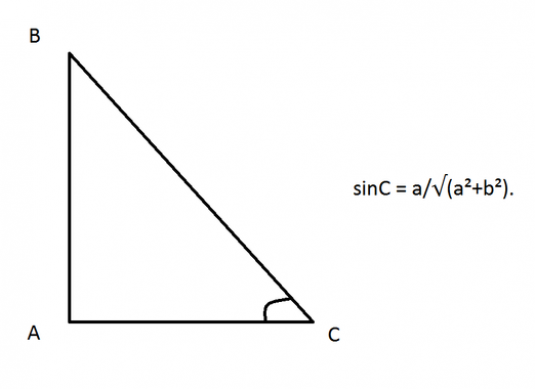Jak znaleźć przeciwprostokątną?

Na samym początku przypominamy, że trójkąt to wielościan z 3 rogami. Jak znaleźć przeciwprostokątną trójkąta prostokątnego, jeśli znane są inne wartości tego trójkąta?

Instrukcje

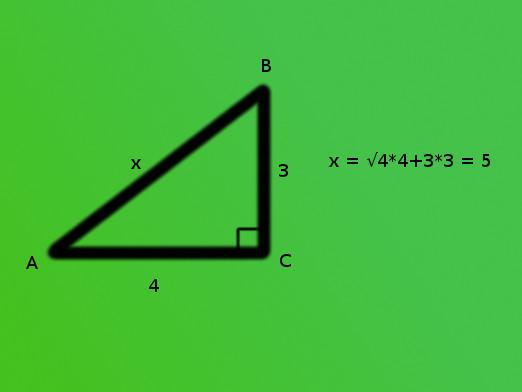
1. Długość nóg są znane. W tym przypadku przeciwprostokątna może być obliczona przy pomocy twierdzenia Pitagorasa. Twierdzenie to brzmi tak: suma kwadratów nóg jest równa kwadratowi przeciwprostokątnej. Z tego wynika, że ​​w celu obliczenia długości przeciwprostokątnej konieczne jest wyrównywanie ilości każdej nogi w kwadracie jeden po drugim. Następnie wynikowe liczby sumują się, az ogólnego wyniku już wyodrębniamy pierwiastek kwadratowy.
2. Jak znaleźć przeciwprostokątną w trójkącie KFB, jeśliczy znana jest cathette (VC) i kąt sąsiadujący z nią? Znany kąt jest oznaczony przez α. Jedna z właściwości trójkąta prostokątnego jest następująca: stosunek długości odnogi prawego trójkąta do długości przeciwprostokątnej jest równy cosinusowi kąta między przeciwprostokątną a tą nogą. Możesz zapisać to w następujący sposób: FB = BK * cos (α).
3. Znany jest inny katetus (KF) i ten sam kątα, Teraz będzie odwrotnie. Hipotenezę można również znaleźć, stosując te same właściwości w trójkącie prostokątnym. Tutaj otrzymujemy, stosunek długości nogi prostokąta trójkątnego do długości jego przeciwprostokątnej jest równy sinusowi kąta naprzeciwko nogi. Zapis: FB = KF * sin (α).
4. Jak znaleźć przeciwprostokątną trójkąta, jeśliOpisuje okrąg, w którym znany jest jego promień. Z właściwości koła, które jest opisane wokół trójkąta prostokątnego, wiadomo, że w takim okręgu środek pokrywa się z punktem przeciwprostokątnej, która dzieli go na pół. Innymi słowy, promień jest połową przeciwprostokątnej. Oznacza to, że dwa promienie tworzą przeciwprostokątną: FB = 2 * R.

Znając właściwości trójkąta prostokątnego uTwierdzenie Pitagorasa bardzo łatwo obliczyć długość przeciwprostokątnej. Jeśli nadal trudno jest zapamiętać wszystkie właściwości, po prostu naucz się gotowych formuł, w których bardzo łatwo podstawić znane wartości, aby obliczyć długość przeciwprostokątnej.