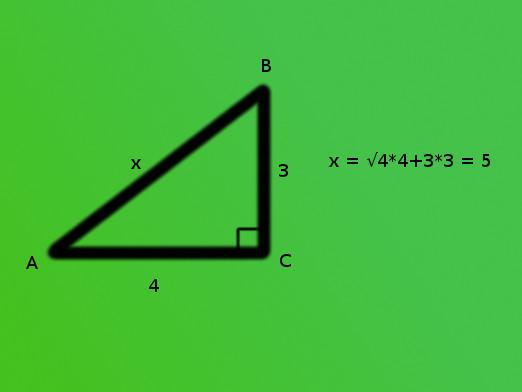
Jak znaleźć bok prawego trójkąta?

Geometria jest jedną z najbardziej złożonych nauk w szkoleprogram. Być może najtrudniejszy dla tych, którzy szukają rozwiązania problemów geometrycznych. W tym przypadku najbardziej poprawnym podejściem jest wyraźnie zaplanowany algorytm działań. Otóż, odpowiednio, znajomość wzorów i twierdzeń. Przy rozwiązywaniu problemów związanych z poszukiwaniem nieznanej strony trójkąta prostokątnego ważne jest prawidłowe użycie warunków początkowych i twierdzenia Pitagorasa. Ponadto ważna jest znajomość właściwości trójkąta prostokątnego. Przykłady najczęstszych warunków problemów z tej serii znajdziesz w tym artykule.

Znajdźmy stronę trójkąta prostokątnego

Jak wiadomo, po stronie prostokątaTrójkąt może być katetusem lub przeciwprostokątną. Znając określone warunki, można obliczyć zarówno cathet, jak i przeciwprostokątną, odpowiadając w ten sposób na główne pytanie: jak znaleźć bok trójkąta prostokątnego. Uwzględniamy te warunki i odpowiednie rozwiązania.

1. Stan: znana jest długość obu nóg. Przeciwprostokątna może być obliczona przy użyciu twierdzenia Pitagorasa. Dla tych, którzy zapomnieli jakie jest to twierdzenie, przypomnij: kwadrat przeciwprostokątny jest równy sumie kwadratów nóg. Biorąc pod uwagę tę wiedzę. które otrzymaliśmy z twierdzenia, tworzymy równanie: FB2 = BK2 + KF2, gdzie FB jest przeciwprostokątną, a BK i KF są nogami. Szukając długości przeciwprostokątnej, należy wyrównać każdy z wymiarów nóg po kolei. Następnie dodaj wynikowe liczby, a na podstawie wyniku obliczymy pierwiastek kwadratowy.
2. Stan: Znana jest katechia i kąt, który jest do niej. Ten kąt jest utworzony przez przeciwprostokątną i nogę, do której jest przymocowany. Oznaczamy znany kąt przez symbol a. Zgodnie z właściwością trójkąta prostokątnego, zapisujemy odpowiedź w następujący sposób: FB = BK * cos (a)
3. Stan: Znany jest cathette (KF) i ten sam kąt a, który tym razem znajduje się w pozycji przeciwnej do nogi. Poszukując w tym przypadku przeciwprostokątnej, pomoże nam własność trójkąta prostokątnego, mówiąc, że stosunek długości nogi do długości przeciwprostokątnej jest równy kątowi sinusowemu przeciwnemu do nogi. Piszemy to w ten sposób: FB = KF * sin (a).
4. Warunek: Znana przeciwprostokątna. Weź prawy trójkąt ABC, gdzie przeciwprostokątna jest AC. Musimy określić kąt c wierzchołkiem w punkcie A jako La, a kąt z wierzchołkiem w punkcie B będzie oznaczony jako Lb. Następnie musimy znaleźć długość nóg AB i BC.
5. Stan: Znana jest katechina z trójkąta prostokątnego. Możemy założyć, że BC jest równe b. W tym przypadku używamy twierdzenia znanego nam Pitagorasa (a ^ 2 + b ^ 2 = c ^ 2). Z równania otrzymujemy wymagany catet | AB | = a = √ (c ^ 2 - b ^ 2).

Znając twierdzenie Pitagorasa, jak widać,Wykonuj te pozornie trudne zadania w Geometrii i niezależnie rozumiesz, jak znaleźć stronę prostokąta prostokątnego. Jeśli nie wiesz, wiesz jak korzystać z twierdzenia Pitagorasa, możesz użyć gotowych formuł.