Znaki równoległości linii prostych
Można udowodnić równoległość dwóch liniipodstawie twierdzenia, zgodnie z którym dwie prostopadłe prostopadłe do jednej prostej będą równoległe. Istnieją pewne oznaki paralelizmu linii - jest ich tylko trzy, a wszystkie z nich rozważymy dokładniej.
Pierwsza oznaka paralelizmu
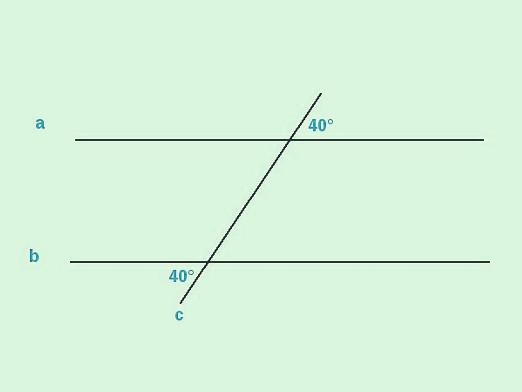
Proste linie są równoległe, jeśli na przecięciu ich trzeciej linii prostej, uformowane kąty wewnętrzne leżące w przeciwnym kierunku będą równe.
Załóżmy, że przekraczamy linie AB i CD liniiza pomocą linii EF utworzono kąty I1 i I2. Są równe, ponieważ linia prosta EF przechodzi pod jednym nachyleniem w stosunku do pozostałych dwóch linii prostych. Na przecięciu linii kładziemy punkty Ki L - uzyskaliśmy segment siecznego EF. Znajdujemy jego środek i umieszczamy punkt O (ryc. 189).

Na linii AB obniżamy prostopadłość z punktu O. Nazywamy to OM. Kontynuuj prostopadłe aż do przecięcia z prostą CD. W rezultacie pierwotna linia AB jest ściśle prostopadła do MN, co oznacza, że CD_ | _MN, ale to stwierdzenie wymaga dowodu. W wyniku prostopadłego i przecięcia linii utworzyliśmy dwa trójkąty. Jedna z nich jest moja, druga to NOC. Rozważmy je bardziej szczegółowo. znaki równoległości linii 7 klasy
Te trójkąty są równe, ponieważ wZgodnie z warunkami twierdzenia, / 1 = / 2, i zgodnie z konstrukcją trójkątów, bok OK = strona OL. Kąt MOL = / NOK, ponieważ są to kąty pionowe. Wynika z tego, że bok i dwa kąty sąsiadujące z jednym z trójkątów są odpowiednio równe bokowi i dwu kątom sąsiadującym z nim, a drugi z trójkątów. Zatem trójkąt MOL = trójkątNOK, a więc kąt LMO = róg KNO, ale wiemy, że LMO jest proste, stąd odpowiadający kąt KNO jest również linią prostą. Oznacza to, że udało nam się udowodnić, że do linii MN zarówno linia AB, jak i prosta linia CD są prostopadłe. Oznacza to, że AB i CD względem siebie są równoległe. To właśnie musieliśmy udowodnić. Rozważ pozostałe znaki równoległych linii (klasa 7), które różnią się od pierwszej cechy metodą dowodową.
Drugi znak równoległości
Zgodnie z drugim znakiem równoległości linii prostych,musimy udowodnić, że kąty uzyskane podczas przecięcia równoległych linii AB i CD linii EF są równe. Tak więc znaki równoległości dwóch linii prostych, zarówno pierwszej, jak i drugiej, oparte są na równości kątów uzyskanych, gdy przecinają się z trzecią linią. Zakładamy, że / 3 = / 2, a kąt 1 = / 3, ponieważ jest do niego pionowy. Zatem f2 będzie równy kątowi 1, ale należy wziąć pod uwagę, że zarówno kąt 1, jak i kąt 2 są kątami wewnętrznymi, poprzecznymi. Dlatego pozostaje nam zastosować naszą wiedzę, a mianowicie, że dwa segmenty będą równoległe, jeśli na ich przecięciu, trzecia prosta, uformowane, wzajemnie sąsiadujące kąty są równe. W ten sposób stwierdziliśmy, że AB || CD.

Udowodniliśmy, że pod warunkiem równoległości dwóch prostopadłości do jednej linii prostej, zgodnie z odpowiednim twierdzeniem, paralelizm linii jest oczywisty.
Trzeci znak równoległości
Istnieje również trzeci znak paralelizmu,o czym świadczy suma jednostronnych kątów wewnętrznych. Taki dowód funkcji linii równoległych, prowadzi do wniosku, że obie linie są równoległe, jeśli na przecięciu ich trzecia prosta ilość jednostronnie wewnętrzne kąty będą równe 2d. Zobacz rysunek 192.










