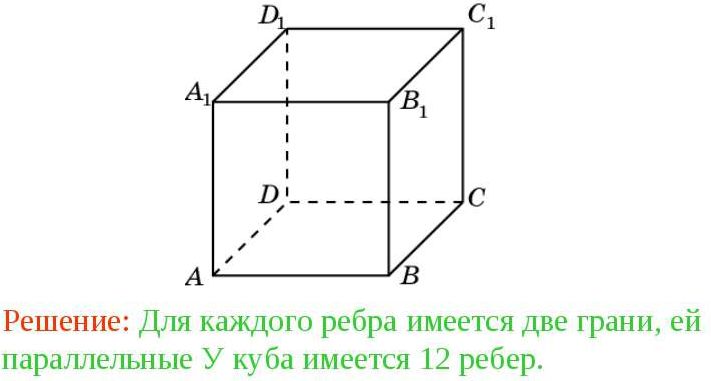
Jak znaleźć krawędź sześcianu?

Kostka jest jednym z najprostszych trójwymiarowychobiekty, zarówno w stereometrii, jak iw naturze. Zanim znajdziesz krawędź sześcianu, musisz przypomnieć sobie, czym jest kostka. Jest to prostokątny równoległościan o równych krawędziach. Ponadto sześcian jest sześciokątem, którego powierzchnie są równe kwadratom. Aby znaleźć krawędź sześcianu, musisz znać jego niektóre parametry - objętość sześcianu, powierzchnię twarzy, długość przekątnej sześcianu lub twarzy.

1. W większości przypadków problemy czterech osóbtypy, w których występuje krawędź sześcianu. Ma on określić długość krawędzi wzdłuż przekątnej sześcianu, wzdłuż przekątnej jego powierzchni, wzdłuż objętości sześcianu i powierzchni twarzy. Najprostszym z nich jest znalezienie krawędzi nad powierzchnią twarzy. W końcu powierzchnia sześcianu jest kwadratem o boku równym krawędzi sześcianu. Dlatego powierzchnia tej ściany jest równa krawędzi sześcianu, podniesiona do kwadratu. Stąd, aby znaleźć krawędź, konieczne jest wyodrębnienie pierwiastka kwadratowego z powierzchni twarzy. a = vS a jest krawędzią sześcianu (długość), S jest obszarem jednej ściany.
2. Jeszcze łatwiej jest znaleźć twarz sześcianu na podstawie jego objętości,ponieważ objętość sześcianu będzie równa konstrukcji długości krawędzi w trzeciej potędze. W konsekwencji, jeśli wyodrębnimy sześcienny pierwiastek (trzeci stopień) z objętości, otrzymamy długość krawędzi a = vV (sześcienny pierwiastek), tutaj a jest krawędzią sześcianu (długość), a V jest jego objętością.
3. Jak znaleźć długość krawędzi sześcianu, jeśli długośćprzekątne. Oznaczamy: a jest krawędzią sześcianu (długość), b jest przekątną powierzchni sześcianu (długość), a c jest przekątną sześcianu (długość). Przekątna krawędzi i powierzchnie sześcianu tworzą równoboczny, prostokątny trójkąt. Stosujemy twierdzenie Pitagorasa, gdzie: a ^ 2 + a ^ 2 = b ^ 2, tutaj (a ^ - potęgowanie) Okazuje się: a = v (b ^ 2/2). Wyodrębniając pierwiastek kwadratowy z połowy kwadratu przekątnej jego powierzchni, znajdujemy długość krawędzi sześcianu.
4. Znajdujemy długość krawędzi wzdłuż przekątnej sześcianu, gdzie a -krawędź sześcianu, b - przekątna ściany, c - przekątna sześcianu. Tworzą prostokątny trójkąt. Zaczynamy od twierdzenia Pitagorasa, gdzie: a ^ 2 + b ^ 2 = c ^ 2. Stosujemy powyższą zależność między wartościami a i b, zastępujemy je wyrażeniem b ^ 2 = a ^ 2 + a ^ 2. Otrzymawszy: a ^ 2 + a ^ 2 + a ^ 2 = c ^ 2, stwierdzamy: 3 * a ^ 2 = c ^ 2, uzyskując skończoną ekspresję; a = v (c ^ 2/3).

Jeśli parametry kostki są ustawione na przestarzałe,krajowe i inne specyficzne jednostki, należy je przetłumaczyć na odpowiednie analogi metryczne - metry sześcienne, decymetry, centymetry lub milimetry.