Jak znaleźć obszar postaci?

Zna i umie policzyć obszary różnychdane są potrzebne nie tylko do rozwiązywania prostych problemów geometrycznych. Nie obywa się bez tej wiedzy i przy sporządzaniu lub sprawdzaniu szacunków dotyczących naprawy lokalu, obliczaniu liczby wymaganych dostaw. Pomyślmy więc, jak znaleźć obszary o różnych liczbach.

Obszar

Część płaszczyzny zamknięta w zamkniętym konturze nazywana jest obszarem tej płaszczyzny. Obszar jest wyrażony liczbą zamkniętych w nim kwadratów.

Aby obliczyć obszar podstawowych kształtów geometrycznych, należy użyć poprawnej formuły.

Obszar trójkąta

Notacja:

• S jest wymaganym obszarem,
• a, b, c są długością boków trójkąta,
• h jest wysokością żądanego trójkąta,
• γ jest kątem między bokiem a i bokiem b,
• r jest promieniem okręgu (wpisanym w trójkąt),
• R oznacza promień okręgu (opisany wokół trójkąta),
• p jest połową obwodu trójkąta.

1. Jeśli h, a są znane, to obszar pożądanego trójkąta jest zdefiniowany jako iloczyn długości boków i wysokości trójkąta spadłego na tę stronę, podzielonego na pół: S = (a · h) / 2
2. Jeśli a, b, c są znane, to wymagany obszarobliczana wzorem Heron: kwadrat brane produktu z połowy obwodu trójkąta korzeni lub trzy różnice pół i obwód każdego z boków trójkąta: S = V (p ° (p - a) · (s - b) · (p - c)).
3. Jeśli a, b, γ są znane, to obszar trójkąta jest zdefiniowany jako połowa iloczynu 2 boków pomnożona przez wartość kąta zatoki między tymi bokami: S = (a · b · sin γ) / 2
4. Jeśli a, b, c, R są znane, to pożądany obszar jest definiowany jako iloczyn długości wszystkich boków trójkąta przez cztery promienie wyznaczonego okręgu: S = (a · b · c) / 4R
5. Jeśli znane są p, r, to wymagany obszar trójkąta jest określany przez pomnożenie połowy obwodu przez promień wpisanego w niego okręgu: S = p · r

Kwadrat kwadratu

Notacja:

• S jest wymaganym obszarem,
• a jest długością boku,
• d jest długością przekątnej.

1. Jeśli strona jest znana, to powierzchnia tej figury jest określona jako kwadrat jej długości boku: S = a²
2. Jeśli d jest znane, to kwadrat kwadratu jest zdefiniowany jako połowa kwadratu długości przekątnej: S = d²/ 2

Powierzchnia prostokąta

Notacja:

• S jest obszarem, który należy określić,
• a, b są długością boków prostokąta.

1. Jeśli a, b są znane, to powierzchnia tego prostokąta jest określona przez iloczyn długości dwóch jego boków: S = a · b
2. Jeśli długości boków są nieznane, to obszar prostokąta musi być podzielony na trójkąty. W tym przypadku obszar prostokąta definiuje się jako sumę obszarów jego trójkątów składowych.

Obszar równoległoboku

Notacja:

• S jest wymaganym obszarem,
• a, b to długości boków,
• h jest długością wysokości tego równoległoboku,
• d1, d2 są długościami dwóch przekątnych,
• α to kąt między bokami,
• γ jest kątem między przekątnymi.

1. Jeżeli znamy a, h, pożądany jest określony poprzez pomnożenie długości boków, a wysokość jest opuszczona na tej stronie s = A · h
2. Jeżeli znane są a, b, α, to obszar równoległoboku określa się przez pomnożenie długości boków równoległoboku i wartości sinusoidalnej kąta między tymi bokami: S = a · b · sin α
3. Jeśli wiemy, że d₁, d₂, γ, wówczas obszar równoległoboku jest zdefiniowany jako połowa iloczynu długości przekątnej i wartości sinusoidalnej kąta między tymi przekątnymi: S = (d₁· D₂· Sinγ) / 2

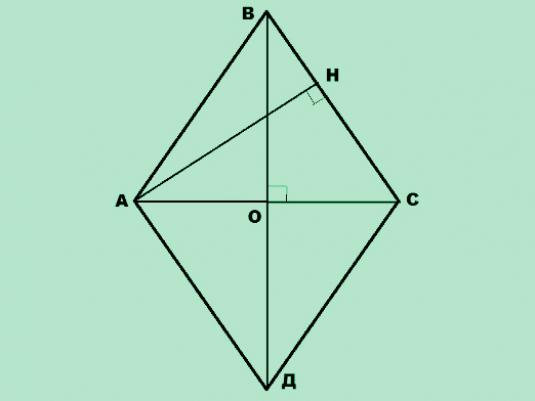
Diamond Square

Notacja:

• S jest wymaganym obszarem,
• a jest długością boku,
• h jest długością wysokości,
• α to mniejszy kąt między dwoma bokami,
• d1, d2 są długościami dwóch przekątnych.

1. Jeżeli znamy a, h, długości rombu jest określany przez pomnożenie powierzchni na długości wysokości boku, który jest pominięty w tym zakresie: s = A · h
2. Jeśli a, α są znane, to obszar rombowy określa się przez pomnożenie kwadratu długości boku przez sinus kąta między bokami: S = a²· Sin α
3. Jeśli wiemy, że d₁ i d₂, następnie wymagany obszar jest zdefiniowany jako połowa iloczynu długości diamentów rombu: S = (d₁· D₂) / 2

Obszar trapezu

Notacja:

• S jest wymaganym obszarem,
• a, b - długości 2 zasad trapezu,
• c, d są długościami lewej i prawej strony trapezu,
• h jest wysokością trapezu,

1. Jeżeli znamy a, b, c, d, żądany obszar jest określony wzorem: A = (a + b) / 2 * √ [c²- (((b-a)²+ c²-d²) / (2 (b-a))²].
2. Dla znanych a, b, h, wymagany obszar jest określony jako iloczyn połowy sumy zasad i wysokości trapezu: S = (a + b) / 2 · h

Powierzchnia wypukłego czworokąta

Notacja:

• S jest wymaganym obszarem,
• d₁, d₂ - długości przekątnych danego czworoboku,
• α to kąt między przekątnymi,
• P = (a + b + c + d) / 2 - połowę obwodu czworokątem wypukłym
• a, b, c, d - długość każdej stronie wypukłego elementu czworobocznego,
• θ = (α + β) / 2 jest połową sumy dwóch przeciwnych kątów wypukłego czworokąta,
• r jest promieniem okręgu wpisanego w wypukły czworobok.

1. Jeśli wiemy, że d₁, d₂, a, obszar wypukłego czworoboku jest zdefiniowany jako połowa iloczynu przekątnych czworoboku pomnożonego przez kąt zatoki między tymi przekątnymi: S = (d₁· D ₂· Sin α) / 2
2. Dla znanego p, r, obszar czworokąta wypukłego definiuje się jako iloczyn pół-wymiaru czworokąta przez promień okręgu wpisanego w czworoboczny: S = p · r
3. Jeśli a, b, c, d, θ są znane, to obszar wypukłyczworobok jest zdefiniowana jako pierwiastek kwadratowy różnicy semiperimeter pracuje, a długość każdego z produktów z ujemną stroną długość wszystkich boków kwadratu i kosinusa połowę sumy dwóch przeciwległych rogach S² = (p - a) (p - b) (p - c) (p - d) - abcd · cos²((α + β) / 2)

Powierzchnia okręgu

Notacja:

• S jest wymaganym obszarem,
• r jest długością promienia,
• d jest długością średnicy.

Jeśli r jest znane, to pożądany obszar jest definiowany jako iloczyn liczby π przez promień w kwadracie: S = π r²

Jeśli d jest znane, to pole koła definiuje się jako iloczyn liczby π przez kwadrat średnicy, podzielonej przez cztery: S = (π · d²) / 4

Obszar złożonej figury

Złożoną można podzielić na proste figury geometryczne. Obszar złożonej figury definiuje się jako sumę lub różnicę obszarów składowych. Weźmy na przykład pierścionek.

Oznaczenie:

• S jest obszarem pierścienia,
• R, r to promienie zewnętrznego obwodu i wewnętrznego, odpowiednio,
• D, d to średnice zewnętrznego koła i wewnętrznego obwodu, odpowiednio.

Aby znaleźć obszar pierścienia, konieczne jest zabranie tego obszaru

mniejsze koło. S = S1-S2 = πR²-rr² = π (R²-r²).

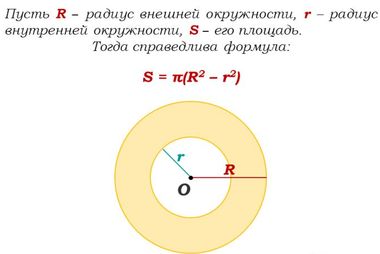
Zatem, jeśli R i r są znane, to obszar pierścienia jest zdefiniowany jako różnica kwadratów promieni koła zewnętrznego i wewnętrznego pomnożona przez liczbę pi: S = π (R²-r²).

Jeśli D i d są znane, to powierzchnia pierścienia jest określona jako jedna czwarta różnicy w kwadratach średnic koła zewnętrznego i wewnętrznego pomnożona przez liczbę pi: S = (1/4) (D²-d²) π.

Obszar cieniowanej sylwetki

Załóżmy, że jest inny (B) (mniejszy) wewnątrz tego samego kwadratu (A), i musimy znaleźć zacienione wgłębienie między cyframi "A" i "B". Powiedzmy "ramkę" małego kwadratu. Aby to zrobić:

1. Znajdujemy obszar na figurze "A" (obliczonej przez wzór na znalezienie kwadratu kwadratu).
2. Podobnie znajdujemy obszar na figurze "B".
3. Odejmujemy obszar "B" od obszaru "A". I tak dostajemy obszar cieniowanej postaci.

Teraz wiesz, jak znaleźć obszary o różnych kształtach.